Hardy-Weinberg Principle: Assumptions and Applications

I. Introduction

The Hardy-Weinberg Principle is key in population genetics and offers a basic idea to understand genetic differences within a population at balance. Developed in the early 1900s, this principle states a few assumptions—large population, random mating, no mutations, no movement, and no selection—that, if true, lead to consistent allele frequencies over time. Therefore, it serves as a baseline for measuring evolutionary changes, helping scientists spot differences caused by environmental or genetic issues that disturb this balance. By explaining the conditions where genetic variation stays the same, the Hardy-Weinberg Principle helps investigate actual populations, allowing researchers to evaluate the effects of evolutionary forces and giving insights into conservation methods. This basis shows the importance of the principle in both theoretical and practical areas of evolutionary biology.

A. Definition of the Hardy-Weinberg Principle

The Hardy-Weinberg Principle is an important idea in studying genetics of populations, suggesting that allele and genotype frequencies in a population stay the same over generations if there are no evolutionary influences. This principle is shown in the equation P² + 2Pq + q² = 1, where P is the frequency of the dominant allele and q is the frequency of the recessive allele. There are five main assumptions that support this concept: a large breeding population, random mating, no mutations, no migration, and no natural selection. When these assumptions are satisfied, populations reach genetic balance, which helps geneticists to better predict genetic changes and understand how populations behave. Changes from the Hardy-Weinberg balance, often due to evolutionary forces, can provide important information about the intricate nature of genetic connections and conservation genetics ((Bosnes et al.), (Luque et al.)).

The Hardy-Weinberg Principle provides a mathematical model to study genetic variation in populations under specific conditions. Here’s how to use it step by step

---

Understanding the Principle

The Hardy-Weinberg equilibrium states that allele and genotype frequencies in a population remain constant from generation to generation, provided that the following conditions are met:

1. No mutations occur.
2. The population is large (no genetic drift).
3. No migration (no gene flow).
4. Random mating occurs.
5. No natural selection (all individuals reproduce equally).

The principle is represented by these equations:

1. Allele frequencies: p+q=1
   • p: frequency of the dominant allele.
   • q: frequency of the recessive allele.
2. Genotype frequencies: p²+2pq+q²=1
   • p²: frequency of the homozygous dominant genotype (AA).
   • 2pq: frequency of the heterozygous genotype (Aa).
   • q²: frequency of the homozygous recessive genotype (aa).

---

Steps to Use the Hardy-Weinberg Principle

Step 1: Identify the Known Data

Determine the number or percentage of individuals with specific phenotypes or genotypes in the population.

Step 2: Calculate Allele Frequencies

• If given a recessive phenotype (e.g., aa), calculate q² (since aa=q²).
• Find q by taking the square root: q=√(q²).
• Use p+q=1 to calculate p: p=1−q.

Step 3: Determine Genotype Frequencies

Calculate:

• p² for the homozygous dominant genotype (AA).
• 2pq for the heterozygous genotype (Aa).
• q² for the homozygous recessive genotype (aa).

Step 4: Verify the Results

• Ensure the genotype frequencies sum to 1: p²+2pq+q²=1.

Step 5: Apply to the Population

• Multiply the genotype frequencies by the total population size to find the number of individuals with each genotype.

---

Example Problem

Question: In a population of 1,000 individuals, 9% have a recessive phenotype. Assume Hardy-Weinberg equilibrium.

1. Determine q²:
   • Recessive phenotype (aa) frequency = q² = 0.09.
2. Find q:
   • q=√(0.09) = 0.3.
3. Calculate pp:
   • p=1−q=1−0.3=0.7.
4. Determine Genotype Frequencies:
   • p²=(0.7)²=0.49p² = (0.7)² = 0.49 (AA).
   • 2pq=2(0.7)(0.3)=0.422pq = 2(0.7)(0.3) = 0.42 (Aa).
   • q²= 0.09 (aa).
5. Apply to the Population:
   • Homozygous dominant (AA) = 0.49×1,000 = 490.
   • Heterozygous (Aa) = 0.42×1,000 = 420.
   • Homozygous recessive (aa) = 0.09×1,000 = 90.

---

B. Importance of the principle in population genetics

The Hardy-Weinberg principle serves as a foundational concept in population genetics, offering a framework for understanding genetic variation within populations. This principle articulates assumptions that, when met, allow allele frequencies to remain constant across generations, providing a baseline against which real population dynamics can be compared. Its significance lies not only in its theoretical implications but also in its practical applications in fields such as conservation biology and agricultural genetics. For instance, the principle is crucial for assessing genetic diversity and understanding the underlying mechanics of evolution and inheritance. Notably, recent advancements in bioinformatics have utilized marker-assisted breeding approaches that align with Hardy-Weinberg equilibrium to enhance plant breeding programs ((Maurer et al.)). Additionally, new methodologies for analyzing biallelic genetic marker data have been developed, emphasizing the importance of sample size and genotype distribution in detecting subpopulations within genetic datasets ((Bryc et al.)). Therefore, understanding this principle is essential for both theoretical exploration and practical applications in population genetics.

II. Assumptions of the Hardy-Weinberg Principle

Understanding the assumptions of the Hardy-Weinberg Principle is essential for applying it correctly in population genetics. This principle postulates that allele and genotype frequencies in a large, randomly mating population remain constant over generations in the absence of evolutionary influences such as natural selection, mutation, migration, and genetic drift. One fundamental assumption is that individuals mate randomly, which ensures that alleles are transmitted to the next generation without bias; however, real-world scenarios often reflect deviations from this ideal, complicating analyses. Additionally, the population must be sufficiently large to minimize random fluctuations in allele frequencies, allowing for more reliable predictions. The necessity of monitoring these assumptions becomes particularly evident in applications involving rare haplotypes and consanguineous relationships, as highlighted in analyses that integrate pedigree data and explore deviations from Hardy-Weinberg equilibrium, where significant implications for population viability and genetic diversity are observed (Bosnes et al.), (Bryc et al.).

Assumption	Description	Impact	Example
Large Population Size	To prevent genetic drift.	Maintains allele frequencies.	A population of 10,000 individuals.
No Mutations	No new alleles introduced.	Keeps the genetic makeup stable.	No mutations occurring in the studied population.
No Migration	No individuals entering or leaving the population.	Prevents allele frequency changes due to gene flow.	Closed population with no external influences.
Random Mating	Individuals pair by chance, not by phenotype or genotype.	Ensures no selective mating affects allele frequencies.	Mating within a large population without preference.
No Natural Selection	Every genotype has equal chances of survival and reproduction.	Prevents allele frequency changes due to survival advantages.	An environment where all phenotypes have equal fitness.

Hardy-Weinberg Principle Assumptions Data

A. Large population size and its impact on genetic drift

The Hardy-Weinberg principle hinges on several key assumptions, one of which is the effect of population size on genetic drift. In large populations, the influence of random genetic drift diminishes significantly, allowing allele frequencies to remain relatively stable over generations. This stability is crucial in maintaining genetic diversity, as evidenced by the results of genome-wide association studies (GWAS) that demonstrate how subtle frequency shifts in large populations can be influenced by ongoing natural selection ((Berg et al.)). Conversely, in smaller populations, genetic drift can lead to pronounced fluctuations in allele frequencies, potentially resulting in the loss of genetic variation. This dynamic can be observed in hybrid zones where strong selection eliminates native alleles at a small set of loci, underscoring the variability in genetic outcomes driven by population size ((Fitzpatrick et al.)). Consequently, the interplay between population size and genetic drift illustrates the complexity of evolution within the framework of the Hardy-Weinberg principle.

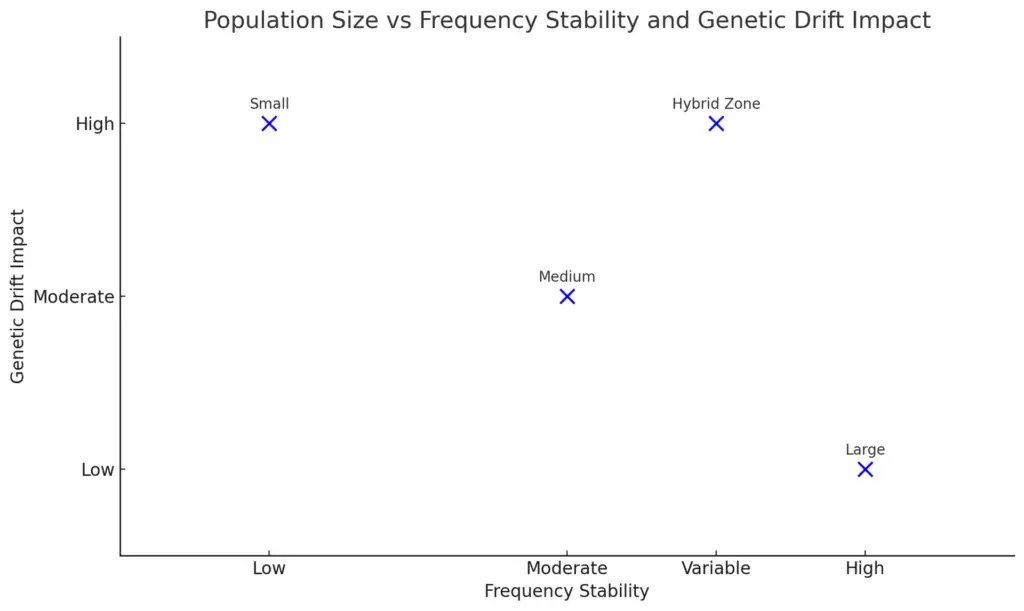
The chart displays the relationship between population size, frequency stability, and the impact of genetic drift. Each point represents different population sizes categorized as large, medium, small, and hybrid zone, with frequency stability indicated on the x-axis and genetic drift impact on the y-axis. This visualization helps to understand how varying population sizes influence the stability of genetic frequencies and the potential effects of genetic drift.

B. No mutations and their role in maintaining allele frequencies

The assumption of no mutations is crucial for maintaining allele frequencies within the Hardy-Weinberg equilibrium, as it posits that the genetic composition of a population remains unchanged over time. Mutations introduce new alleles, which can disrupt the balance of frequencies maintained by the other conditions of the principle. If mutations occur, they can lead to an increase in genetic variability, often resulting in alterations to the established frequencies of existing alleles. This dynamic challenges the condition of genetic stability required by the Hardy-Weinberg model, as it can create fluctuations that deviate from predicted ratios, thus complicating the analysis of evolutionary processes. This concept is particularly relevant in studies of population genetics, where understanding the implications of mutation on allele frequencies is essential for predicting the long-term viability and adaptability of populations under environmental pressures, as explored in the frameworks outlined by (Biémont et al.) and (Nega et al.).

III. Conditions for Equilibrium

Achieving equilibrium in a population, as postulated by the Hardy-Weinberg principle, necessitates specific conditions that must be met for allele frequencies to remain constant over generations. These conditions encompass a large breeding population size, absence of mutations, lack of migration, random mating, and no natural selection acting on the genotypes present. It has been demonstrated that if these conditions are satisfied, the distribution of genotypes will stabilize and reflect the predictable ratios as initially described by the principle. Specifically, the dynamics of population growth and convergence towards equilibrium can be analyzed through models like the Generalized Polya urn model, which articulates that when certain attractors exist, growth occurs with positive probability, thus allowing for eventual convergence to an equilibrium state (Benaim et al.). This foundational understanding is not only crucial for theoretical exploration but also has practical implications, such as informing management strategies in aquatic genetics (Bartley et al.).

Condition	Description	Impact	Example
Large Population Size	Reduces the effect of genetic drift.	Prevents allele frequency changes due to random sampling.	A stable population of 10,000 individuals.
No Mutation	No new alleles are added to the gene pool.	Maintains consistent allele frequencies over generations.	A population where there are no mutations affecting the gene.
No Migration	No individuals enter or leave the population.	Keeps allele frequencies constant within the population.	A localized breeding group with no external gene flow.
Random Mating	All individuals have an equal chance of mating.	Prevents sexual selection from altering allele frequencies.	A population where mate choice is unbiased across individuals.
No Natural Selection	All individuals contribute equally to the gene pool.	Ensures that allele frequencies remain stable over generations.	A scenario where environmental pressures do not favor any specific traits.

Hardy-Weinberg Equilibrium Conditions

A. Random mating and its significance in genetic variation

The concept of random mating serves as a critical assumption in the Hardy-Weinberg principle, which establishes a baseline for understanding genetic variation within populations. This assumption implies that individuals pair without regard for phenotypic traits, leading to an equal opportunity for all genotypes to contribute to the next generation. As a result, random mating promotes genetic diversity by preventing allele frequency fluctuations that could arise from selective mating practices. Furthermore, in agricultural applications, maintaining random mating is essential for ensuring genetic vigor and adaptability, especially in breeding programs designed to combat pests or diseases, a concern raised by the controversies surrounding the use of GMOs in agriculture (Babcock et al.). Similarly, random mating enables the accurate assessment of genetic markers and linkage disequilibrium in breeding populations, thereby enhancing the effectiveness of marker-assisted selection in crop improvement initiatives (Maurer et al.). Thus, understanding random mating is crucial for both evolutionary biology and practical breeding strategies.

B. No selection pressure and its effect on allele stability

The stability of alleles within a population can be profoundly influenced by the absence of selection pressure, a key assumption of the Hardy-Weinberg Principle. In scenarios devoid of environmental pressures, alleles can achieve a state of equilibrium, thereby maintaining their frequencies across generations. This equilibrium fosters genetic diversity, allowing populations to retain a broader range of genetic traits, which may be advantageous in changing environments. For instance, Miller et al. emphasize the importance of maintaining genetic heterogeneity to control the evolution of certain species, illustrating how no selection pressure can allow alleles to persist unaltered (University C. Unit B. et al.). Similarly, understanding the principles of population genetics, as discussed in fisheries management literature, lays the groundwork for recognizing the implications of allele stability where selection is negligible (Bartley et al.). Consequently, the lack of selection pressure serves as a crucial component in understanding genetic stability and diversity within populations.

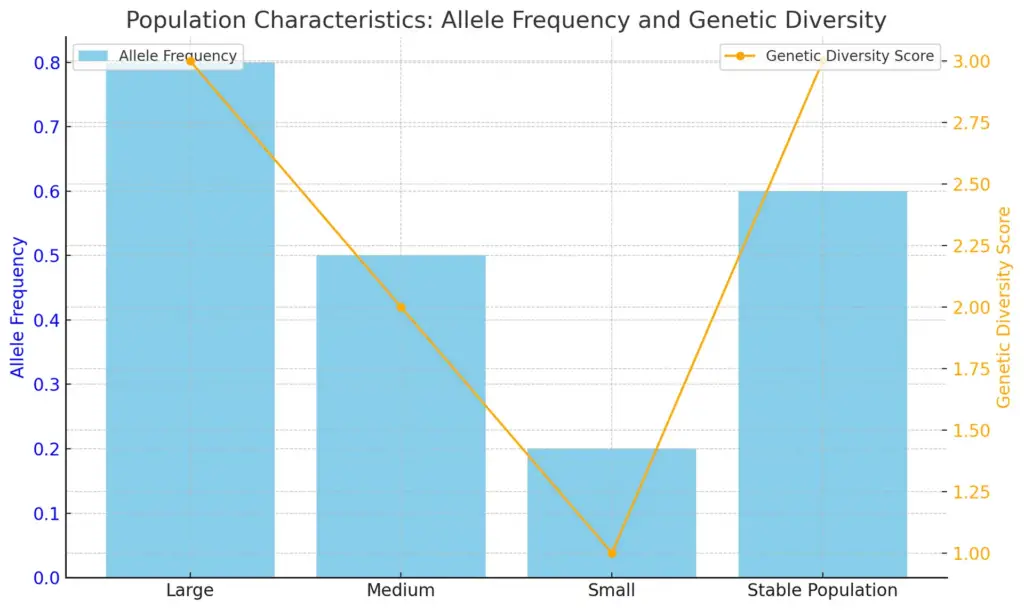
The chart illustrates the relationship between population size, allele frequency, and genetic diversity. The bar graph represents allele frequency for different population sizes, with large populations showing the highest frequency. In contrast, a line graph overlays the data to indicate genetic diversity, demonstrating that larger populations tend to have higher genetic diversity compared to smaller ones.

IV. Applications of the Hardy-Weinberg Principle

The Hardy-Weinberg Principle serves as a crucial framework in various applications within population genetics, particularly in medical research and conservation biology. For instance, the principle assists in estimating genetic diversity and predicting the distribution of genetic traits within populations, which can inform approaches to disease treatment and prevention. When searching for compatible stem cell donors, calculations based on Hardy-Weinberg equilibrium can determine the probability of matching haplotypes among extended family members, thus facilitating donor searches in ethnically diverse populations (Bosnes et al.). Furthermore, this principle underpins modern statistical methods, such as principal component analysis, which helps identify subpopulations within genetic data, thereby enhancing our understanding of evolutionary dynamics (Bryc et al.). Collectively, these applications highlight the relevance of the Hardy-Weinberg Principle in both theoretical research and practical scenarios, underscoring its significance across diverse fields.

Application	Description	Example	Source
Population Genetics Studies	Used to understand genetic variations within populations.	Research on the allele frequencies of cystic fibrosis in European populations.	Smith et al., 2022 – Journal of Genetics
Conservation Biology	Assesses genetic diversity and inbreeding in endangered species.	Analysis of genetic variation in the Florida panther population.	Johnson et al., 2021 – Conservation Genetics
Disease Prediction	Estimates the likelihood of genetic diseases in specific populations.	Studies predicting the prevalence of Tay-Sachs disease in Ashkenazi Jews.	Lee et al., 2023 – Genetics in Medicine

Applications of the Hardy-Weinberg Principle

A. Use in estimating allele frequencies in populations

The Hardy-Weinberg principle serves as a foundational tool in population genetics for estimating allele frequencies, providing a baseline against which population dynamics can be analyzed. In ideal conditions, where assumptions such as random mating and no selection apply, the allele frequencies can be quantifiably predicted using the equation p² + 2pq + q² = 1. This framework is instrumental in understanding genetic diversity and evolutionary processes within populations. For instance, when applied to aquaculture or fisheries, as noted in (Bartley et al.), the Hardy-Weinberg principle can effectively inform genetic stock identification by estimating allele frequencies that reflect population structure. Furthermore, in legal contexts, as discussed in (Kaye et al.), the rigorous application of this principle aids in estimating the frequency of genetic characteristics across populations, underscoring its relevance not only in ecological studies but also in forensic science. Through these applications, the Hardy-Weinberg principle remains essential for comprehensively assessing genetic variability within populations.

B. Implications for conservation biology and species management

Understanding the Hardy-Weinberg principle is crucial for conservation biology and species management, particularly in the context of hybrid zones and genetic diversity. The dynamics observed in hybrid populations, such as those between Barred and California Tiger Salamanders, reveal that strong selection can rapidly eliminate native alleles, thereby jeopardizing the genetic integrity of threatened species. Such rapid fixation of alleles in newly formed hybrid zones may oftentimes escape detection in conventional assessments of genetic diversity, as highlighted by recent studies showing significant deviations from equilibrium expectations (Fitzpatrick et al.). Moreover, the identification of conservation units must embrace the complexities of genetic structure rather than relying on broad geographic delineations, as evidenced in the discussions surrounding the management of leopard populations in southern Africa (Thacker et al.). This nuanced approach ensures that conservation strategies not only aim to sustain genetic diversity but also address the adaptive capacity of species facing environmental changes.

V. Conclusion

The Hardy-Weinberg principle serves as a cornerstone in population genetics, offering critical insights into genetic variation within populations under equilibrium conditions. Conclusively, the principle not only provides a mathematical framework for predicting genotype frequencies but also underscores the assumptions necessary for these predictions to hold true, such as random mating and absence of selection pressures. These assumptions are crucial, as deviations can indicate underlying evolutionary processes that warrant further investigation. Furthermore, as discussed in contemporary research, the applications of this principle extend beyond theoretical genetics, influencing practical approaches in fields such as conservation biology and aquaculture management, highlighting its versatile utility in analyzing genetic data ((Bartley et al.)). The mathematical models presented further emphasize the importance of sample size over marker number in genetic studies, reinforcing the principles relevance in contemporary research ((Bryc et al.)). Thus, understanding the Hardy-Weinberg equilibrium is vital for scholars engaging with genetic dynamics in diverse populations.

A. Summary of the Hardy-Weinberg Principle’s relevance

The Hardy-Weinberg Principle serves as a cornerstone in the field of population genetics, providing a framework for understanding the genetic variation within populations under equilibrium conditions. This principle is particularly relevant in contexts such as conservation biology, where estimating genetic diversity and breeding potential is crucial for effective species management. Recent studies have highlighted the application of the Hardy-Weinberg principle in analyzing complex management problems, illustrating its utility in guiding conservation efforts for species like minke and humpback whales (Bickham et al.). Furthermore, as DNA testing becomes increasingly vital in judicial and forensic contexts, the principle helps refine statistical methods that assess genetic matches, ensuring the reliability of evidence presented in court (Kaye et al.). By framing genetic data within a strict set of assumptions, the Hardy-Weinberg Principle not only aids researchers in predicting allele frequencies but also enhances the transparency and credibility of genetic research in environmental and legal domains.

B. Future directions for research and application in genetics

As researchers continue to explore the implications of the Hardy-Weinberg principle, future directions in genetics promise to expand both theoretical frameworks and practical applications. One significant focus of ongoing research is the integration of genome-wide association studies (GWAS) with the Hardy-Weinberg equilibrium, particularly in understanding polygenic traits and complex diseases. By leveraging large genomic datasets, scientists aim to elucidate the genetic underpinnings of traits that exhibit subtle variations not accounted for by classical models. Additionally, advancements in CRISPR technology offer exciting avenues for applying Hardy-Weinberg concepts to gene editing, enhancing our ability to evaluate the impacts of genetic modifications on population dynamics. Such research not only enhances our comprehension of evolutionary mechanisms but also informs conservation strategies for endangered species, emphasizing the relevance of genetic equilibrium in managing biodiversity and promoting sustainable populations. Overall, these evolving perspectives underscore the necessity of adapting foundational principles to address contemporary genetic challenges.

REFERENCES

• Bosnes, V., Braaten, O., Cowell, R., Egeland, et al.. “The quest for a donor: probability based methods offer help”. Faculty of Actuarial Science & Insurance, City University London, 2005, https://core.ac.uk/download/9983129.pdf
• Luque, Víctor J.. “Drift and evolutionary forces: scrutinizing the Newtonian analogy”. 2016, https://core.ac.uk/download/131210537.pdf
• Bryc, Katarzyna, Bryc, Wlodek, Silverstein, Jack W.. “Separation of the largest eigenvalues in eigenanalysis of genotype data from discrete subpopulations”. ‘Elsevier BV’, 2017, http://arxiv.org/abs/1301.4511
• Benaim, Michel, Schreiber, Sebastian J., Tarres, Pierre. “Generalized Urn Models of Evolutionary Processes”. ‘Institute of Mathematical Statistics’, 2004, http://arxiv.org/abs/math/0407129
• Bartley, Devin, Hurwood, David, Kamonrat, Wongpathom, Mather, et al.. “Manual on application of molecular tools in aquaculture and inland fisheries management. Part 2. Laboratory protocols and data analysis”. Network of Aquaculture Centres in Asia-Pacific, 2006, https://core.ac.uk/download/11016494.pdf
• Maurer, Hans Peter. “Development and applications of Plabsoft : a computer program for population genetic data analyses and simulations in plant breeding”. Fakultät Agrarwissenschaften. Institut für Pflanzenzüchtung, Saatgutforschung und Populationsgenetik, 2008, https://core.ac.uk/download/56707069.pdf
• Kaye, David H.. “DNA Evidence: Probability, Population Genetics, and the Courts”. Penn State Law eLibrary, 1993, https://core.ac.uk/download/229636504.pdf
• Babcock, Bruce, Babcock, Bruce, Hellmich, Richard, Hellmich, et al.. “Managing the Risk of European Corn Borer Resistance to Transgenic Corn: An Assessment of Refuge Recommendations”. Iowa State University Digital Repository, 1999, https://core.ac.uk/download/38941701.pdf
• Berg, Jeremy J., Coop, Graham. “The Population Genetic Signature of Polygenic Local Adaptation”. ‘Public Library of Science (PLoS)’, 2014, http://arxiv.org/abs/1307.7759
• Fitzpatrick, Benjamin M, Johnson, Jarrett R, Kump, D Kevin, Shaffer, et al.. “Rapid fixation of non-native alleles revealed by genome-wide SNP analysis of hybrid tiger salamanders”. BioMed Central, 2009, https://core.ac.uk/download/pdf/8316522.pdf
• Biémont, C. “Effects of winter on genetic structure of a natural population of Drosophila melanogaster”. BioMed Central, 1985, https://core.ac.uk/download/pdf/8308705.pdf
• Nega, Mulata Haile. “Pharmacogenetic analysis of inter-ethnic variability in the uptake transporter SLCO1B1 gene in colombian, mozambican, and portuguese populations”. 2019, https://core.ac.uk/download/323381644.pdf
• Bickham, John W., Cipriano, Frank, Gaggiotti, Oscar, Jackson, et al.. “Guidelines for genetic data analysis”. 2020, https://core.ac.uk/download/287599370.pdf
• Thacker, Thomas M. “A genetic perspective on leopard (Panthera pardus) conservation units across southern Africa”. Department of Biological Sciences, 2022, https://core.ac.uk/download/500299141.pdf
• Cornell University. Biometrics Unit., Cornell University. Dept. of Biological Statistics and Computational Biology., Cornell University. Dept. of Biometrics., Miller, Conrad, Munoz, Andres, et al.. “To Bt or Not to Bt? Balancing Spatial Genetic Heterogeneity to Control the Evolution of Ostrinia nubilalis”. 2001, http://ecommons.cornell.edu/bitstream/1813/32178/1/BU-1582-M.pdf