Population Growth Models: Exponential vs Logistic

I. Introduction

Understanding models of population growth is important for knowing how ecosystems work and how species survive in different environments. This essay looks at two main models: exponential and logistic growth, which show different ways that populations change. Exponential growth, shown by a J-shaped curve, happens in perfect conditions where resources are endless, allowing populations to grow quickly over time. On the other hand, logistic growth considers carrying capacity, where environmental limits slow down growth as populations near a saturation point, resulting in an S-shaped curve. This difference in growth patterns highlights the role of resource availability and the larger effects on population management and conservation. By studying these models, we can better understand the complexities of population dynamics and their importance for ecological balance and biodiversity. Graphs of these models will make it easier to see how they apply in real-world situations.

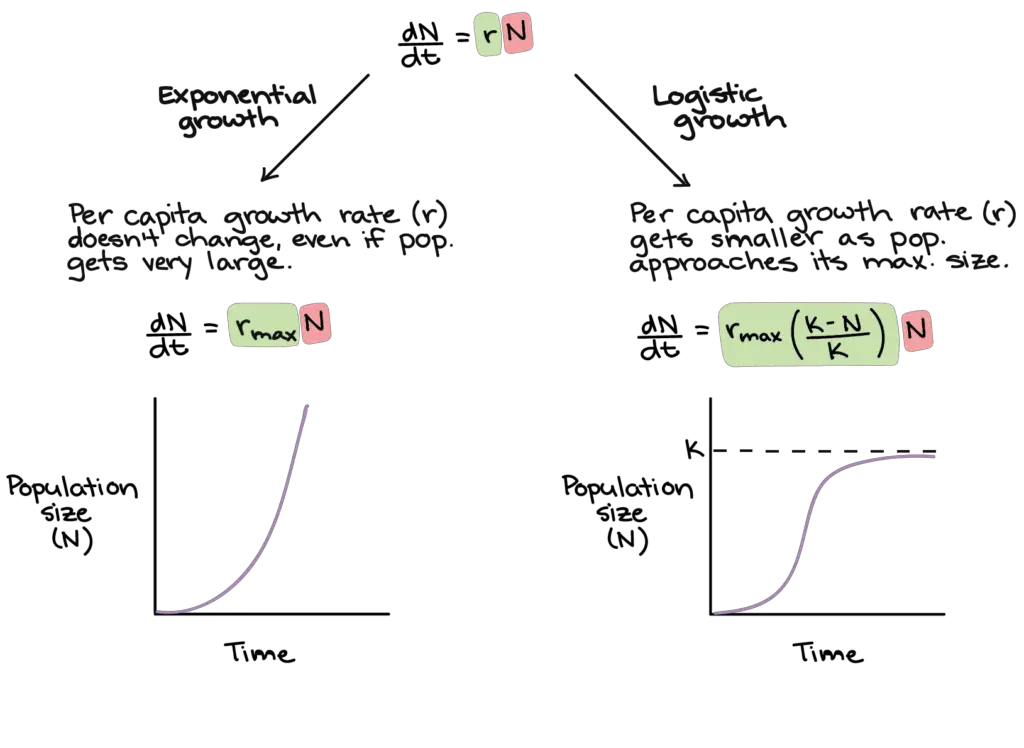
Image 2 : Comparison of Exponential and Logistic Population Growth Models

A. Definition of population growth models

Understanding models for population growth is very important for studying ecology and environmental science because these models help us predict how populations change over time due to different factors. The two main models, exponential and logistic growth, have different uses. Exponential growth, shown by the equation dN/dt = rN, describes a situation where resources are endless, allowing populations to increase at a steady rate no matter their size. On the other hand, logistic growth, which can be written as dN/dt = rmax * (K-N)/K * N, takes into account environmental limits, especially carrying capacity (K), which causes the growth rate to slow down as the population size gets closer to this limit. This important difference emphasizes the importance of (Keppens et al.) in understanding ecological systems and (Tsoularis et al.) that points out the limits of traditional models, thus providing crucial insights into population changes and their effects on biodiversity and resource management.

Model	Definition	Characteristics	Equation	Example Species
Exponential Growth	A model of population growth that assumes a constant rate of increase over time, resulting in a rapid increase as the population base grows.	Unlimited resources, ideal conditions, individual reproduction rates remain consistent.	N(t) = N0 * e^(rt)	Bacteria, certain insects
Logistic Growth	A model of population growth that accounts for carrying capacity, showing how population growth slows as it approaches this limit.	Limited resources, environmental resistance, stabilizes at carrying capacity.	N(t) = (K * N0) / (N0 + (K – N0) * e^(-rt))	Large mammals, plants

Population Growth Models Comparison

B. Importance of understanding growth models in ecology and resource management

Understanding growth models is very important for both ecological studies and resource management across different fields. Knowing the difference between exponential and logistic growth models gives key insights into how populations behave, especially in areas like pest control and wildlife management, where it is necessary to predict how different species act. For example, (Ferguson et al.) shows that understanding the density-dependent relationships in species such as Anopheles gambiae can improve our ability to predict outcomes in vector control, emphasizing the need for resource strategies that match these growth patterns. Furthermore, grasping these models is increasingly important because of how ecosystems are connected and the impact of human activities. Programs that stress quantitative skills in ecology highlight that understanding these models helps students and professionals critically analyze data and predictions. This skill allows them to “engage like scientists” in their evaluations and management strategies, as pointed out in (Trenckmann et al.). Applying these basic theories helps deepen the understanding of ecological relationships, enabling managers to adopt sustainable practices informed by data and proactive planning. By considering ecological balance and resource availability, this knowledge ultimately leads to better decision-making. This is vital for tackling modern environmental issues and ensuring that both natural resources and biodiversity remain sustainable over time.

II. Exponential Growth Model

The Exponential Growth Model says that populations can grow really fast when conditions are good, showing a J-shaped curve often seen in the beginning stages of population growth. This model relies on the idea that there are endless resources, allowing continuous reproduction without limits; as the population gets bigger, more individuals can reproduce, causing rapid increases. Recent research, noted in (MP K et al.), indicates that while the model works well during early growth periods, it reveals a key problem: it cannot support endless growth in a limited environment. Additionally, similar trends have been found in viral populations, which initially grow exponentially but are later slowed down by outside factors like changes in behavior or treatment methods, as shown in the study detailed in (Clewley et al.). This situation highlights the need to move to more complex models, like the Logistic Growth Model, for understanding long-term population changes.

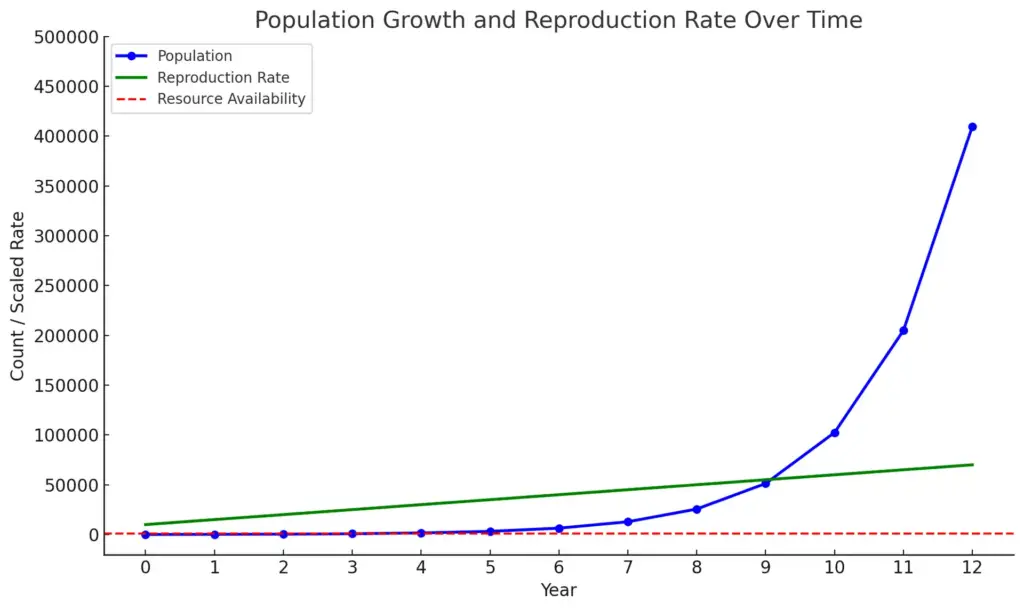
The chart illustrates the population growth and reproduction rate over time from year 0 to year 12. The blue line represents the population, which exhibits exponential growth, while the green line indicates the reproduction rate, showing a steady increase. The red dashed line denotes the constant resource availability, which remains unchanged throughout the years. This visualization effectively highlights the disparity between population growth and fixed resource availability.

A. Characteristics and mathematical representation of exponential growth

Exponential growth is a foundational concept in population dynamics, distinctly characterized by its rapid increase as the population size escalates without any limiting factors. This remarkable phenomenon can lead to astonishing increases in population numbers over relatively short periods, presenting a clear illustration of how organisms can thrive under optimal conditions. Mathematically represented by the equation dN/dt = rN, where N denotes the population size and r symbolizes the intrinsic growth rate, this model underscores the notion that the per capita growth rate remains constant irrespective of the population’s current size. This constancy implies that even as populations grow larger, the rate at which they continue to grow does not diminish, allowing for exponential populations to theoretically double in a fixed time interval. This principle leads to the formation of J-shaped growth curves that signify unchecked proliferation, highlighting the potential for explosive population surges. However, it is essential to recognize that this mathematical representation often assumes ideal conditions which rarely exist in nature. Such assumptions prompt the need for more refined models that incorporate environmental constraints—some of which may mitigate growth—such as the modified SEIR model used in epidemiological studies (cantó et al.). Indeed, understanding the characteristics of exponential growth lays a crucial groundwork for further exploration of logistical limitations in population modeling. This exploration is critical, as demonstrated in studies of marine species growth patterns (Haddon et al.), which illustrate how incorporating real-world factors can lead to more accurate predictions and inform conservation strategies effectively.

B. Real-world examples and implications of exponential growth in populations

The idea of fast population growth is shown clearly by how quickly human populations and some invasive species are increasing. For example, the rise in the global human population from about 1 billion in 1800 to more than 7 billion today shows this trend, especially in the 20th century when improvements in medicine and farming greatly lowered death rates. Likewise, species like the zebra mussel have shown rapid growth after being introduced to new ecosystems, which causes serious ecological issues and financial loss. However, these growth patterns are not just theories; they require careful study since they point to future problems like resource shortage and environmental damage. As discussed in the literature, the long-term health of population dynamics is uncertain because small changes in system factors can lead to different results that challenge previous beliefs about growth stability (Growiec J), (Growiec et al.).

Species	Initial Population	Growth Rate (% per hour)	Time Period (hours)	Final Population
Bacteria (E. coli)	1	100	24	16777216
Housefly	1	200	5	31250
Rabbits	2	300	6	2048
Humans (COVID-19 Infection)	1	60	30	1073741824
Fruit Flies	10	25	10	944

Exponential Population Growth Examples

III. Logistic Growth Model

When looking at the Logistic Growth Model, we see that this model gives a detailed view of how populations change, especially where resources are scarce. In contrast to the Exponential Growth Model, which assumes growth can go on forever, the Logistic Model includes the idea of carrying capacity, which is the biggest number of individuals an ecosystem can support. This model is especially important in real-life situations, like managing fish populations. For example, the study of blacklip abalone in Tasmania shows how the inverse-logistic method can effectively show growth patterns for both young and adult stages (Haddon et al.). Also, efforts to conserve endangered species, like the Devils Hole pupfish, highlight how the Logistic Growth Model can assess extinction risks based on population size, which helps in forming plans to keep populations stable (Beissinger et al.). In conclusion, the Logistic Growth Model is essential for understanding and promoting sustainable populations.

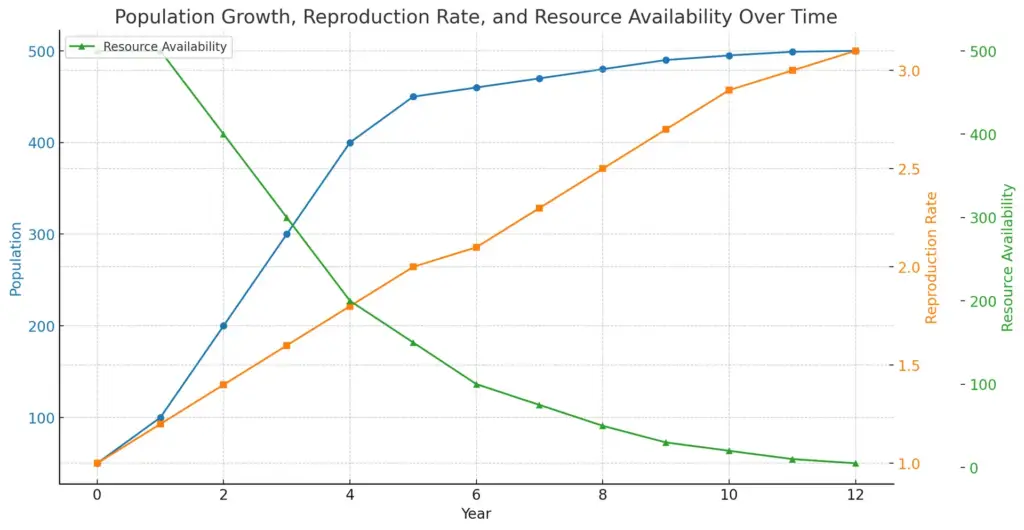
This chart illustrates the trends in population growth, reproduction rate, and resource availability over a span of thirteen years. The blue line represents the population, which shows an increasing trend. The orange line indicates the reproduction rate, which also increases but at a different pace. The green line depicts resource availability, illustrating a significant decrease as the years progress. This visualization helps to understand the relationship between these variables over time.

A. Characteristics and mathematical representation of logistic growth

Logistic growth is characterized by an initial period of rapid increase, where the population expands significantly due to abundant resources and little competition, followed by a gradual leveling off as the population reaches its carrying capacity. This carrying capacity, denoted mathematically by the equation dN/dt = rmax * (K-N)/K * N, is a crucial concept in understanding the limitations imposed by the environment. In this equation, K represents the maximum population size that the environment can sustainably support. As the population approaches this limit, the growth rate, denoted as rmax, begins to diminish due to the increasing competition for limited resources, such as food, space, and other essential necessities. This model effectively contrasts with exponential growth, where the population size continues to rise unchecked, illustrating that resources play a pivotal role in shaping ecological dynamics and population health. Observations from various biological systems, such as the frequency distribution of metastatic tumor colonization—analyzed in studies of cancer progression—demonstrate that logistic growth can be influenced by numerous factors, including environmental constraints and biological interactions. These findings suggest that even processes in disease dynamics may reflect the principles inherent in logistic models (cantó et al.), (Lee et al.). Consequently, understanding logistic growth is fundamental to effectively managing populations and formulating conservation strategies that aim not only to protect species but also to maintain ecological balance. By applying these principles, researchers and conservationists can develop more effective interventions that promote sustainability in ecosystems under threat.

B. Factors influencing the transition from exponential to logistic growth

Understanding the change from exponential to logistic growth means looking at different ecological factors that affect population changes. At first, populations might grow exponentially when there are lots of resources and few environmental limits. But as populations grow, issues like limited resources, competition, and predation become more important. For example, interactions like predation can change population trends by creating non-linear effects based on prey numbers, which can speed up extinction chances for some species (Abrams et al.). Also, the visibility of invasive species can influence management and control strategies, highlighting the need to think about ecological relationships (Cacho et al.). In the end, these interactions are key in controlling growth rates, marking the move from uncontrolled exponential growth to the stabilizing impact of logistic growth when populations reach their carrying capacity.

Factor	Impact	Example	Source
Resource Availability	Limits population size as resources become scarce.	Food supply decreases as population density increases.	United Nations Food and Agriculture Organization (FAO), 2022
Carrying Capacity	Defines the maximum population that an environment can sustain.	Different ecosystems have varying carrying capacities.	Ecological Society of America, 2021
Reproductive Rates	High reproductive rates can lead to brief exponential growth.	Species with rapid reproduction can overshoot carrying capacity.	National Oceanic and Atmospheric Administration (NOAA), 2023
Predation and Competition	Natural checks on population growth through predation or competitive interactions.	Predators increase as prey populations grow, balancing the ecosystem.	Nature Conservancy, 2022
Disease Spread	Illness can significantly reduce population numbers during high-density periods.	Crowded conditions facilitate faster spread of diseases.	Centers for Disease Control and Prevention (CDC), 2023

Factors Influencing the Transition from Exponential to Logistic Growth

IV. Comparison of Exponential and Logistic Growth Models

In looking at how populations change, comparing exponential and logistic growth models shows key insights into how populations react to environmental limits. The exponential growth model, known for its fast, unchecked rise, works under perfect conditions with lots of resources, creating a J-shaped curve that shows constant growth over time. On the other hand, the logistic growth model takes into account limiting factors, which adds a carrying capacity that eventually stops population growth, resulting in an S-shaped curve where growth slows down as the population nears ecological limits. This difference is important when studying real populations, especially in Africa, where different growth rates create serious challenges for planning and resource distribution (Chinaka et al.). Furthermore, new modeling techniques that combine user preferences and ecological differences highlight the complexity of population dynamics beyond simple interactions, stressing the need for flexible frameworks in ecological studies (Keppens et al.).

Model	Description	Equation	Key Characteristics	Example	Limitations
Exponential Growth	Growth that occurs in an ideal environment with unlimited resources.	N(t) = N0 * e^(rt)	Rapid growth; no limits; leads to overshoot.	Bacterial growth in ideal conditions.	Not sustainable in real-world scenarios.
Logistic Growth	Growth that occurs in an environment with limited resources, leading to a carrying capacity.	N(t) = (K * N0) / (N0 + (K – N0) * e^(-rt))	S-shaped curve; growth slows as resources become scarce.	Population of deer in a forest with limited food.	Assumes a constant carrying capacity and can simplify complex ecosystems.

Comparison of Exponential and Logistic Growth Models

A. Key differences in assumptions and outcomes of each model

The basic ideas behind exponential and logistic growth models affect their results in studying populations. Exponential growth thinks that resources are unlimited, allowing populations to grow at a steady rate, which creates a J-shaped curve on a graph displaying population size over time. On the other hand, the logistic model includes the idea of carrying capacity of the environment, resulting in a more realistic S-shaped curve where growth decreases as resources get low. The differences in these ideas impact how we predict population sustainability and managing resources. For example, exponential growth might suggest constant population increases, while logistic growth highlights the resource limits that help keep populations stable within a certain range. This difference is important for assessing ecological actions, as knowing these basic concepts can greatly influence plans for conserving and managing species (Breen et al.), (Baio et al.).

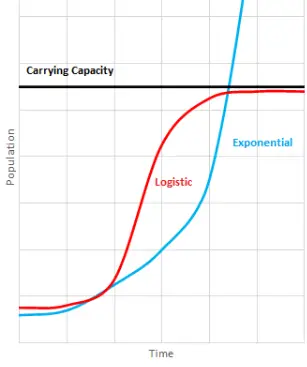
Image1 : Comparison of Logistic and Exponential Population Growth Models

B. Applications and limitations of both models in ecological studies

In ecological studies, exponential and logistic growth models give important information on population changes, even though they have different uses and drawbacks. The exponential model is useful for examining populations in stable settings where there is plenty of resources, which results in fast growth. However, its main drawback is that it does not consider environmental limits, which can lead to inaccurate predictions about real-world populations (cited in ). On the other hand, the logistic model includes carrying capacity, showing a more realistic picture because it considers limiting factors that affect population size. This model is particularly useful in cases like wildlife management and conservation, where knowing the limits of populations is crucial. Still, the logistic model might simplify complex biological interactions and the variability found in natural ecosystems, highlighting the need for models that can incorporate unpredictable factors, as mentioned in (C Besse et al.) and (Sans Aó Rosselló et al.).

Model	Applications	Limitations
Exponential Growth	Ideal for populations with abundant resources and no significant environmental constraints.	Fails to consider carrying capacity; unrealistic in long-term ecological studies.
Logistic Growth	More accurate for natural populations where resources are limited; reflects real-world scenarios.	May oversimplify complex interactions; assumes constant carrying capacity.

Population Growth Models Comparison

V. Conclusion

In looking at the differences between exponential and logistic growth models, we see that these models are important not just in theory but also in their impact on ecological management and biodiversity conservation. Exponential growth shows how populations can expand quickly without limits, revealing how ecosystems can change fast under perfect conditions. However, this type of growth is usually not sustainable, showing the real-world issues like climate change and limited resources, as noted in the study by (Préfontaine et al.). On the other hand, the logistic model brings in the idea of carrying capacity, pointing out that populations cannot keep growing forever due to environmental limits. This model is especially useful in situations where there are species interactions and community dynamics, as explained in (Oremus M et al.). Grasping these different models gives important information to scientists and policymakers for creating plans for sustainable population management amid environmental issues.

A. Summary of key points discussed

When looking at population growth models, the difference between exponential and logistic growth shows key ecological ideas. Exponential growth, shown by a J-shaped curve, means a fast-growing population with no limits, which can lead to taking too many resources. On the other hand, logistic growth takes into account the limits of the environment, shown by an S-shaped curve that levels off as the population gets close to its carrying capacity. To support these models, it is important to think about the basic ideas of ecological competition and resource supply, as noted in (Ekaka-A et al.). Also, new progress in growth modeling shows how updated versions of traditional equations can fix past issues, thus providing a stronger base for studying population changes, as mentioned in (Tsoularis et al.). Visual tools can clearly show these ideas, highlighting the need to grasp both growth types in ecological research and resource management plans.

B. The significance of choosing the appropriate model for population studies

Choosing the right model for studying populations is very important because it greatly affects our understanding of ecology and how we manage resources. Exponential growth models, which show J-shaped curves, think there are endless resources and show how populations can grow quickly when conditions are perfect. On the other hand, logistic growth models consider environmental limits, showing how populations level off as they near their carrying capacity. This difference matters—it influences conservation methods, farming practices, and sustainability efforts. For example, using an exponential model to predict fish numbers in a lake could lead to overfishing, while a logistic model would consider the lake’s ecological limits for a better, more sustainable approach. In the end, choosing the right model can help create better management plans and enhance our understanding of the complex relationships in population ecosystems, highlighting the need for careful study in this field.

References:

• Haddon, Malcolm, Mundy, Craig, Tarbath, David. “Using an inverse-logistic model to describe growth increments of blacklip abalone (Haliotis rubra) in Tasmania”. 2008, https://core.ac.uk/download/11023409.pdf
• Beissinger, Steven. “Digging the pupfish out of its hole: risk analyses to guide harvest of Devils Hole pupfish for captive breeding.”. eScholarship, University of California, 2014, https://core.ac.uk/download/323080983.pdf
• Keppens, J., Shen, Q.. “Compositional Model Repositories via Dynamic Constraint Satisfaction with Order-of-Magnitude Preferences”. ‘AI Access Foundation’, 2011, http://arxiv.org/abs/1107.0035
• Tsoularis, A.. “Analysis of logistic growth models”. ‘Massey University’, 2001, https://core.ac.uk/download/148639061.pdf
• Kashchenko M.P., Kashchenko N.M.. “A majorizing forecast of the earth population in a reduced resource-limited model”. EDP Sciences, 2024, https://core.ac.uk/download/616919273.pdf
• Clewley, J.P., Hué, S., Pillay, D., Pybus, et al.. “Genetic analysis reveals the complex structure of HIV-1 transmission within defined risk groups”. 2005, https://core.ac.uk/download/1669028.pdf
• Ekaka-A, Enu-Obari N.. “Computational and mathematical modelling of plant species interactions in a harsh climate”. University of Liverpool (University of Chester), 2009, https://core.ac.uk/download/364743.pdf
• Abrams, Allesina, Assaf, Bartlett, Bascompte, Black, Brook, et al.. “Predation effects on mean time to extinction under demographic stochasticity”. 2012, http://arxiv.org/abs/1206.0935
• Cacho, Oscar J., Hester, Susan M., Pheloung, Paul, Spring, et al.. “Weed Search and Control: Theory and Application”. 2025, https://core.ac.uk/download/pdf/6667833.pdf
• cantó, cereda, jie guan, kermack, kermack, liangrong, wei. “Modeling the Epidemic Outbreak and Dynamics of COVID-19 in Croatia”. ‘Institute of Electrical and Electronics Engineers (IEEE)’, 2020, http://arxiv.org/abs/2005.01434
• Lee, Steve P., McBride, William H., Qian, Hong, Sun, et al.. “Characterization of Metastatic Tumor Formation by the Colony Size Distribution”. 2006, http://arxiv.org/abs/q-bio/0608024
• C. Besse, O. Goubet, Régis Ferrière, S. Nicaise, T. Goudon, Viet Chi Tran. “Stochastic and deterministic models for age-structured populations with genetically variable traits”. ‘EDP Sciences’, 2009, http://arxiv.org/abs/0809.3767
• Andreu Sansó Rosselló, Antoni Luis Alcover Casasnovas. “The tourist area lifecycle and the unit roots test. A new economic perspective for a classic paradigm in tourism.”. 2025, https://core.ac.uk/download/pdf/6509164.pdf
• Jakub Growiec. “Knife-Edge Conditions in the Modeling of Long-Run Growth Regularities”. 2025, https://core.ac.uk/download/pdf/6922287.pdf
• Growiec, Jakub. “Knife-edge conditions in the modeling of long-run growth regularities”. 2025, https://core.ac.uk/download/pdf/7302761.pdf
• Ferguson, H.M., Killeen, G.F., Knols, B.G.J., Lwetoijera, et al.. “Linking individual phenotype to density-dependent population growth: the influence of body size on the population dynamics of malaria vectors”. ‘The Royal Society’, 2011, https://core.ac.uk/download/110613.pdf
• Trenckmann, Elizabeth. “Development of an Active-Learning Lesson that Targets Student Understanding of Population Growth in Ecology”. DigitalCommons@UMaine, 2017, https://core.ac.uk/download/217066692.pdf
• Breen, David J., Clegg, Andrew J., Colquitt, Jillian, Cunningham, et al.. “The clinical effectiveness and cost-effectiveness of ablative therapies in the management of liver metastases: systematic review and economic evaluation”. 2014,
• Baio, Gianluca, Heath, Anna, Remiro-Azócar, Antonio. “Methods for Population Adjustment with Limited Access to Individual Patient Data: A Review and Simulation Study”. ‘Wiley’, 2021, https://core.ac.uk/download/477687289.pdf
• Préfontaine, Stéphanie. “Réponse métabolique de communautés bactériennes de Sarracenia purpurea provenant d’un gradient latitudinal et exposées à un gradient de température”. ‘Universite de Sherbrooke’, 2020, https://core.ac.uk/download/344753454.pdf
• Mark Oremus, Parminder Raina. “Caregiver Employment Status and Time to Institutionalization of Persons with Dementia”. 2025, https://core.ac.uk/download/pdf/6354890.pdf
• Chinaka, Nduka, Ethelbert, Petronilla, Ogoke, Uchenna. “Comparative Analysis of Population Censuses in Africa”. International Journal of African and Asian Studies, 2016, https://core.ac.uk/download/234690215.pdf

Image References:

• “Comparison of Exponential and Logistic Population Growth Models.” cdn.kastatic.org, 13 January 2025, https://cdn.kastatic.org/ka-perseus-images/69602c1370155fd480bb092161bb963905c5c212.png
• “Comparison of Logistic and Exponential Population Growth Models.” study.com, 13 January 2025, https://study.com/cimages/multimages/16/logistic_growth_curve6788556151222917364.png